Wo Quantencomputer wirklich punkten können
Ein Team um Prof. Dr. Jens Eisert zeigt, dass eine bestimmte Klasse von Optimierungsproblemen durch Quantencomputer schneller gelöst werden kann als mit konventionellen Methoden
Das Problem des Handlungsreisenden ist ein Klassiker in der Mathematik. Ein Reisender soll auf dem kürzesten Weg N Städte besuchen und wieder zum Ausgangspunkt zurückkehren. Mit steigender Anzahl N explodiert die Anzahl der möglichen Routen. Dieses Problem ist dann mit Näherungsverfahren lösbar. Quantenrechner könnten hier rascher deutlich bessere Lösungen liefern. © HZB
Die vorliegende Arbeit (Pfeil) zeigt, dass ein bestimmter Teil der kombinatorischen Probleme mit Quantencomputern sehr viel besser lösbar ist, möglicherweise sogar exakt. © HZB
Das Problem des Handlungsreisenden gilt als Paradebeispiel für kombinatorische Optimierungsprobleme. Nun zeigt ein Berliner Team um den theoretischen Physiker Prof. Dr. Jens Eisert der Freien Universität Berlin, dass eine bestimmte Klasse solcher Probleme tatsächlich durch Quantencomputer besser und sehr viel schneller gelöst werden kann als mit konventionellen Methoden.
Quantencomputer rechnen mit so genannten Qbits, die nicht wie bei konventionellen logischen Schaltungen entweder Null oder Eins betragen, sondern in einem präzisen Sinne alle Werte dazwischen annehmen. Diese Qbits werden durch stark heruntergekühlte Atome, Ionen oder supraleitende Schaltkreise realisiert und es ist physikalisch noch sehr aufwändig, einen Quantencomputer mit vielen Qbits zu bauen. Doch mit mathematischen Methoden lässt sich schon jetzt erforschen, was fehlertolerante Quantencomputer künftig leisten könnten. „Darüber gibt es viele Mythen und zuweilen auch zu einem Grade heiße Luft und Hype. Aber wir haben uns der Frage einmal mit mathematischen Methoden rigoros gestellt und solide Ergebnisse zum Thema geliefert. Vor allem haben wir geklärt, in welchem Sinne es überhaupt Vorteile geben kann“, sagt Prof. Dr. Jens Eisert, der eine gemeinsame Forschungsgruppe an der Freien Universität Berlin und am Helmholtz-Zentrum Berlin leitet.
Als Paradebeispiel dient das bekannte Problem des Handlungsreisenden: Ein Reisender soll eine Anzahl von Städten besuchen und im Anschluss wieder in die Heimatstadt zurückkehren. Wie sieht die kürzeste Route aus? Dieses Problem ist zwar leicht verständlich, aber wird mit steigender Anzahl von Städten immer komplexer, die Rechenzeit explodiert. Das Problem des Handlungsreisenden steht für eine Gruppe von Optimierungsproblemen, die enorme wirtschaftliche Bedeutung haben, ob es um Schienennetze, Logistik oder um die Optimierung von Ressourcen geht. Mit Näherungsverfahren lassen sich gute approximative Lösungen finden.
Das Team um Jens Eisert und seinen Kollegen Jean-Pierre Seifert arbeitete nun rein analytisch, um zu evaluieren, wie ein Quantencomputer mit Qbits diese Klasse von Problemen lösen könnte. Ein klassisches Gedankenexperiment mit Stift und Papier und einer Menge Fachwissen. „Wir nehmen einfach an, unabhängig von der physikalischen Realisierung, dass es ausreichend Qbits gibt, und betrachten die Möglichkeiten, damit Rechenoperationen durchzuführen“, erklärt Vincent Ulitzsch, Doktorand an der Technischen Universität Berlin. Dabei erkannten sie Ähnlichkeiten zu einem bekannten Problem der Kryptographie, also der Verschlüsselung von Daten. „Wir stellten dann fest, dass wir eine Unterklasse dieser Optimierungsprobleme mit dem Shor-Algorithmus behandeln können,“ sagt Ulitzsch. Damit „explodiert“ die Rechenzeit nicht mehr mit der Anzahl der Städte (exponentiell, 2N), sondern steigt nur noch polynomial, also mit Nx, wobei x eine Konstante ist. Die so errechnete Lösung ist außerdem qualitativ deutlich besser als die Näherungslösung mit dem konventionellen Algorithmus.
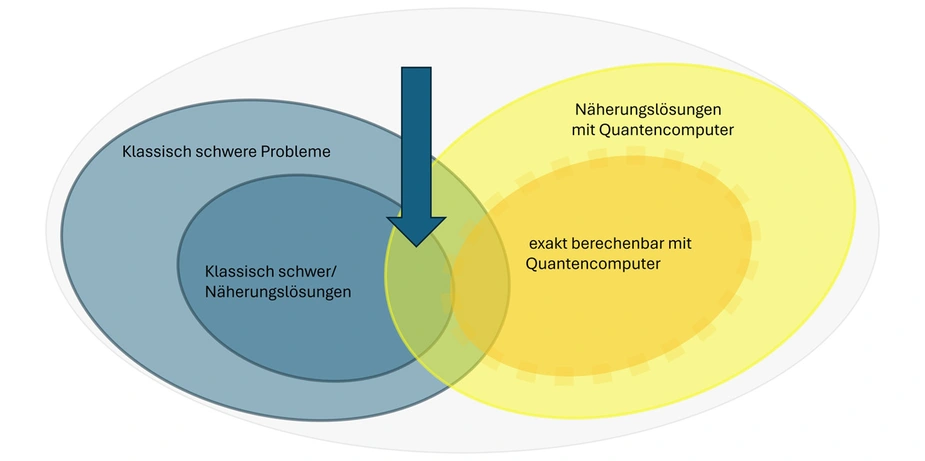
„Wir haben gezeigt, dass Quantencomputer für bestimmte Instanzen des Problems prinzipiell einen Vorteil gegenüber klassischen Computern aufweisen, wenn es um eine bestimmte, aber sehr wichtige und praktisch relevante Klasse kombinatorischer Optimierungsprobleme geht“, sagt Eisert.
Publikation:
Science Advances (2024): An in-principle super-polynomial quantum advantage for approximating combinatorial optimization problems via computational learning theory
Niklas Pirnay, Vincent Ulitzsch, Frederik Wilde, Jens Eisert, Jean-Pierre Seifert
DOI: 10.1126/sciadv.adj5170
Kontakt:
Helmholtz-Zentrum Berlin für Materialien und Energie
Gemeinsame Forschergruppe für Quantenrechnen und -simulation
EM-GQCS-office(at)helmholtz-berlin.de
Dr. Antonia Rötger
Pressestelle
+49 30 8062-43733
antonia.roetger(at)helmholtz-berlin.de
Pressemitteilung HZB vom 15.03.2024